publications

2024

1. 

   Differential Privacy Under Class Imbalance: Methods and Empirical Insights

   Lucas Rosenblatt, Yuliia Lut, Eitan Turok, Marco Avella-Medina, and Rachel Cummings

   International Conference on Machine Learning, 2024

   Abs arXiv Bib Reviews

   Imbalanced learning occurs in classification settings where the distribution of class-labels is highly skewed in the training data, such as when predicting rare diseases or in fraud detection. This class imbalance presents a significant algorithmic challenge, which can be further exacerbated when privacy-preserving techniques such as differential privacy are applied to protect sensitive training data. Our work formalizes these challenges and provides a number of algorithmic solutions. We consider DP variants of pre-processing methods that privately augment the original dataset to reduce the class imbalance; these include oversampling, SMOTE, and private synthetic data generation. We also consider DP variants of in-processing techniques, which adjust the learning algorithm to account for the imbalance; these include model bagging, class-weighted empirical risk minimization and class-weighted deep learning. For each method, we either adapt an existing imbalanced learning technique to the private setting or demonstrate its incompatibility with differential privacy. Finally, we empirically evaluate these privacy-preserving imbalanced learning methods under various data and distributional settings. We find that private synthetic data methods perform well as a data pre-processing step, while class-weighted ERMs are an alternative in higher-dimensional settings where private synthetic data suffers from the curse of dimensionality.

   @article{rosenblatt2024differential,
     title = {Differential Privacy Under Class Imbalance: Methods and Empirical Insights},
     author = {Rosenblatt, Lucas and Lut, Yuliia and Turok, Eitan and Avella-Medina, Marco and Cummings, Rachel},
     year = {2024},
     journal = {International Conference on Machine Learning},
     reviews = {https://openreview.net/forum?id=SgIg3cZjuN}
   }

2. 

   Introducing DBRX: A New State-of-the-Art Open LLM

   The MosaicML Research Team

   2024

   Blog Code

2023

1. 

   Fast hyperboloid decision tree algorithms

   Philippe Chlenski, Ethan Turok, Antonio Moretti, and Itsik Pe’er

   International Conference on Learning Representations, 2023

   Abs arXiv Bib Reviews

   Hyperbolic geometry is gaining traction in machine learning for its effectiveness at capturing hierarchical structures in real-world data. Hyperbolic spaces, where neighborhoods grow exponentially, offer substantial advantages and consistently deliver state-of-the-art results across diverse applications. However, hyperbolic classifiers often grapple with computational challenges. Methods reliant on Riemannian optimization frequently exhibit sluggishness, stemming from the increased computational demands of operations on Riemannian manifolds. In response to these challenges, we present hyperDT, a novel extension of decision tree algorithms into hyperbolic space. Crucially, hyperDT eliminates the need for computationally intensive Riemannian optimization, numerically unstable exponential and logarithmic maps, or pairwise comparisons between points by leveraging inner products to adapt Euclidean decision tree algorithms to hyperbolic space. Our approach is conceptually straightforward and maintains constant-time decision complexity while mitigating the scalability issues inherent in high-dimensional Euclidean spaces. Building upon hyperDT we introduce hyperRF, a hyperbolic random forest model. Extensive benchmarking across diverse datasets underscores the superior performance of these models, providing a swift, precise, accurate, and user-friendly toolkit for hyperbolic data analysis.

   @article{chlenski2023fast,
     title = {Fast hyperboloid decision tree algorithms},
     author = {Chlenski, Philippe and Turok, Ethan and Moretti, Antonio and Pe'er, Itsik},
     year = {2023},
     journal = {International Conference on Learning Representations},
     reviews = {https://openreview.net/forum?id=TTonmgTT9X}
   }

2. 

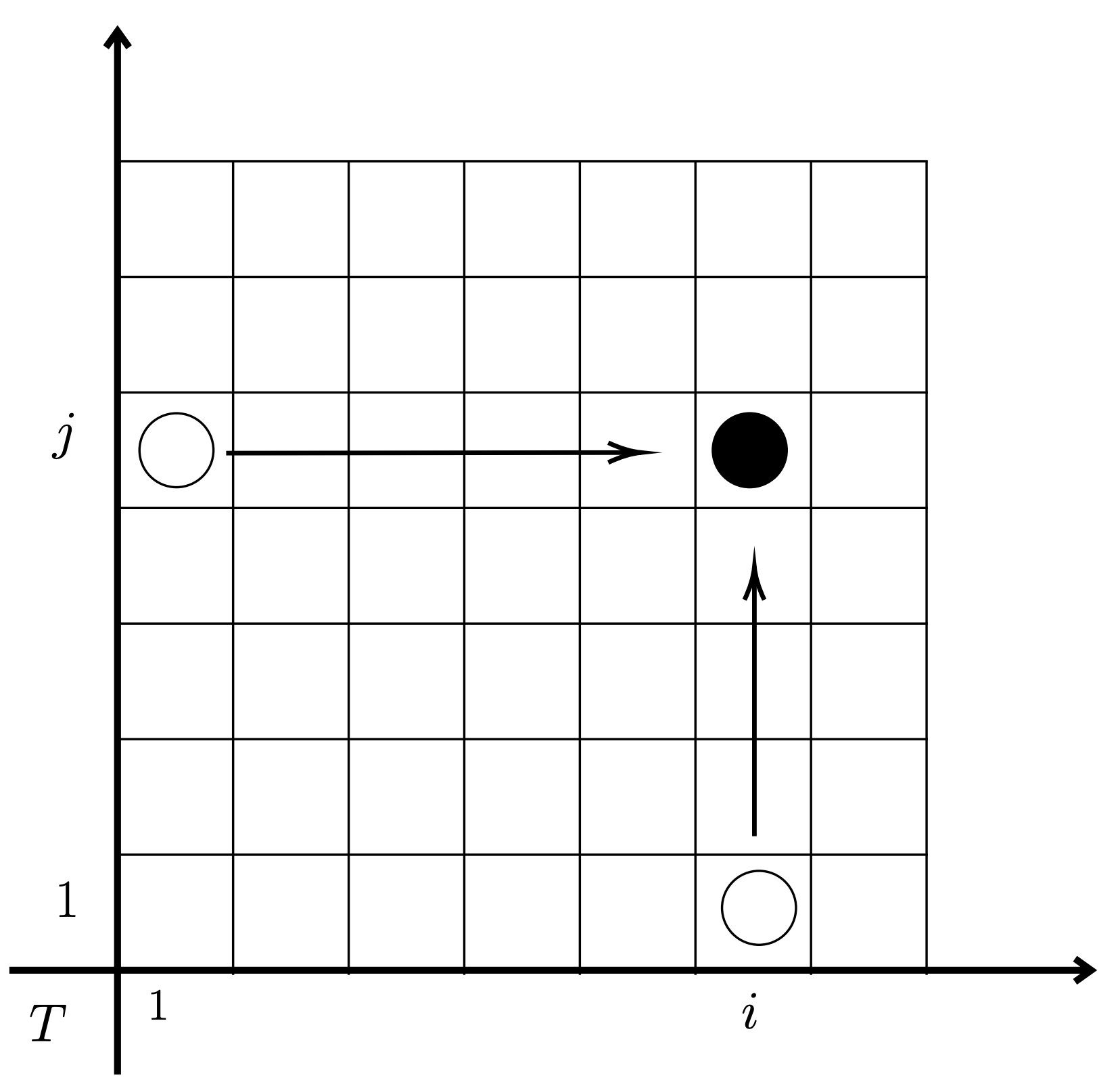   Tensors Ranks and the Fine-Grained Complexity of Dynamic Programming

   Josh Alman, Ethan Turok, Hantao Yu, and Hengzhi Zhang

   Innovations in Theoretical Computer Science, 2023

   Abs arXiv Bib Reviews

   Generalizing work of Künnemann, Paturi, and Schneider [ICALP 2017], we study a wide class of high-dimensional dynamic programming (DP) problems in which one must find the shortest path between two points in a high-dimensional grid given a tensor of transition costs between nodes in the grid. This captures many classical problems which are solved using DP such as the knapsack problem, the airplane refueling problem, and the minimal-weight polygon triangulation problem. We observe that for many of these problems, the tensor naturally has low tensor rank or low slice rank. We then give new algorithms and a web of fine-grained reductions to tightly determine the complexity of these problems. For instance, we show that a polynomial speedup over the DP algorithm is possible when the tensor rank is a constant or the slice rank is 1, but that such a speedup is impossible if the tensor rank is slightly super-constant (assuming SETH) or the slice rank is at least 3 (assuming the APSP conjecture). We find that this characterizes the known complexities for many of these problems, and in some cases leads to new faster algorithms.

   @article{alman2023tensors,
     title = {Tensors Ranks and the Fine-Grained Complexity of Dynamic Programming},
     author = {Alman, Josh and Turok, Ethan and Yu, Hantao and Zhang, Hengzhi},
     year = {2023},
     journal = {Innovations in Theoretical Computer Science},
     reviews = {https://github.com/eitanturok/eitanturok.github.io/blob/master/assets/markdown/Tensor%20Ranks%20and%20the%20Fine-Grained%20Complexity%20of%20Dynamic%20Programming/reviews.md}
   }